Isn't it fun what programmers consider a "normal human being".
GNSS and time
Published: 2023-03
I recently had the pleasure™ of dealing with time, in particular with how it is represented inside computers and inside the GNSS (Global Navigation Satellite System). What initially seemed a reasonably straightforward problem ended up in a surprisingly deep rabbit hole involving atomic clocks, leap seconds, a metrology and computer-history lesson focusing on the narrow period between 1970 and 1972 and a short dive into the Linux kernel code.
This post is the summary of what I found while researching this topic.
Disclaimer
This topic turned out to be rather intricate and figuring out the "technically correct" answer became a personal challenge (which, as a friend of mine correctly pointed out, is a polite way of describing an obsession).
Luckly, 90% of the details reported below are irrelevant unless you need to handle timestamps before 1972 with second-level (or higher) precision. This blog post assumes that you are a normal human being that only needs to convert UTC timestamps to UNIX timestamps/GPS timestamps after 1972, and therefore presents a simplified model of reality, correct enough for the assumed use case.
Whenever this blog post makes a technically incorrect but practically correct enough statement, that statement will end with an asterisk (*). At the end of the blog post there's a section that describes what actually happened to time between 1970 and 1972.
Background: representing time
How can time be expressed as bits of information that can be processed by a computer?
First of all, we need to differentiate between two concepts: "time point" and "duration". A time point (often called "timestamp") is, as the name suggets, a precise point in time (e.g. the "1st of October 2004 at 14:32:13 in the Europe/Rome timezone"). On the other hand, a duration represents an extent of time (e.g. "5 seconds"). These two concepts can also be represented on a timeline:
These two concepts can also be combined in a somewhat intuitive "time arithmetic":
time point + time point = undefined
time point + duration = time point
time point - time point = duration
duration ± duration = durationDurations are relatively easy to represent in a computer: you can use a normal numerical variable and by convention say that it represents a duration of a certain number of (e.g.) milliseconds. Durations behave like other scalar quantities (length, weigth, ...) and can be managed as such. The only part that requires some attention is when mixing durations using different SI ratios, for example when summing a duration in milliseconds with one in seconds.
On the other side, time points are more difficult. An intuitive approach could be to use the same
representation commonly used by humans, which in this post I will call the "wall-clock" representation.
An example of such representation could be 21/04/1975 12:17:00.
The computer could store each piece independently (one variable for the day number, one for the month
number, ...) and then combine them together when they have to be shown to the user. This approach is the one
used by the C's tm struct
(docs) and by Javascript's
Date
(docs).
This approach has the clear advantage of being easy for humans to understand, but it has several shortcomings:
- It's not clear what timezone is being used. The same representation could map to different points on the time line depending on whether it is expressed in one timezone or another. And timezones are a source of a lot of headaches.
- A basic implementation of the wall-clock representation makes it trivial to represent invalid time points. For example, assuming that a normal integer variable is used internally to represent the number of days, one could set its value to 16245, which in most calendars is not a valid day number. Even assuming that we can afford the performance penalty required to ensure that only valid value are used, implementing such checks is definitely not trivial (if you are curious about why watch this or look up what happened on the 5th of October 1582).
- A basic implementation of the wall-clock representation is quite wasteful memory-wise, requiring around six integer variables to represent a single time point.
Luckly, we can do better. Nowadays, most computer systems have converged on a representation based
on an "epoch" (a precise time point taken as a reference) and a duration of time elapsed
from that epoch. As far as this post is concerned, each epoch defines a new "time reference system", which
in this post will be called "clock" (for analogy with the std::chrono
C++ library).
As a mental model, each "clock" can be tough of as a way of giving a different "label" to a particular instant on the time line.
For example, let's consider the POSIX clock (often called UNIX time). It defines its epoch to be the
01-01-1970 00:00:00 UTC, which precisely identifies a single
time point (*). Once the epoch is fixed, a POSIX time point can be expressed as a duration (e.g. a number
of seconds) elapsed before or after that epoch. For example, a POSIX time point of
15 seconds would represent the time point
01-01-1970 00:00:15 UTC (*).
Technically, from what I understand, the POSIX standard only talks about seconds after the POSIX epoch, but the concept can be easily extended to arbitrary durations (milliseconds, nanoseconds, ...) after or before the epoch. A negative duration would express a time point before the epoch.
This representation, although less amenable to humans, counters all the disadvantages of the wall-clock representation. Timezones are not a problem, as the epochs are usually defined using UTC time points. Moreover, invalid dates are not representable, as any duration before/after the epoch is by definition a valid date. Finally, each time point can be represented by a single value (e.g. the number of milliseconds after the epoch), leading to a way more compact representation.
As an additional bonus, computing how much time is elapsed between two time points expressed as epoch+duration is efficient, as it involves a single difference (assimung they share the same epoch). With the wall-clock representation this computation is significantly more complicated.
Background: leap seconds
Until here, we have conveniently ignored a piece of the puzzle: leap seconds.
Understanding leap seconds requires undestanding the various ways that humans have figured out to decide how long a second is. Historically, the length of a second has been determined from astronomical references. Using modern lexicon, this way of determining the length of a second is called UT1, and has two big drawbacks: astronomical references are difficult to measure precisely and, more importantly, the duration of a UT1 second is tied to Earth's rotational speed. This would not be a huge problem if it wasn't for the fact that Earth's rotational speed is not constant, and tends to progressively slow down over time.
This is a simplification, and a detailed explanation of UT1 and UT0 is beyond the scope of this post.
As the required precision for time keeping grew, the variability in length of a UT1 second started being a problem. This led to the development of a new definition of the second, based on precisely measurable and, more importantly, unchanging atomic properties. This new definition of the second resulted in the creation of the Internation Atomic Time (TAI for short), which is independent from Earth's rotational speed and the messiness of astronomical references. This new time scale soon became the "default" for scientific applications.
Given the differences in their definitions, these TAI and UT1 time scales get progressively "out of sync" with each other, because UT1 progressively falls behind TAI due to Earth's slowing rotation. By itself this would not be a problem, but it becomes one if we tried to use TAI as a "universal human time". Humans activities continue to follow the sun cycle, and would therefore like to remain in UT1. If TAI became the "universal human time", over centuries the difference between TAI and UT1 would start to become meaningful, and it could potentially end up in a situation in which a human clock would show a time of 14:00:00 (two o'clock in the afternoon, in TAI) but the sun would have already set (because it would be 21:00:00, nine o'clock in the evening, in UT1).
This is of course not desirable, and the "solution" was the creation of a new time scale, UTC (Coordinated Universal Time), which is designed to bridge the difference between TAI and UT1. The main idea is that one UTC second would always equal to one TAI second (*), but periodically an integer number of seconds would added (or potentially removed) from UTC so that the difference between UT1 and UTC remains below one seconds (*). In symbols:
\[ UTC = TAI + n \]
\[ \vert UT1 - UTC \vert < 0.9 \, seconds \]
Where \(n\) is the integer number of leap seconds (*).
The relationship between UT1 and UTC can also be seen in the following plot, where the vertical jumps show the addition of a leap second (source):
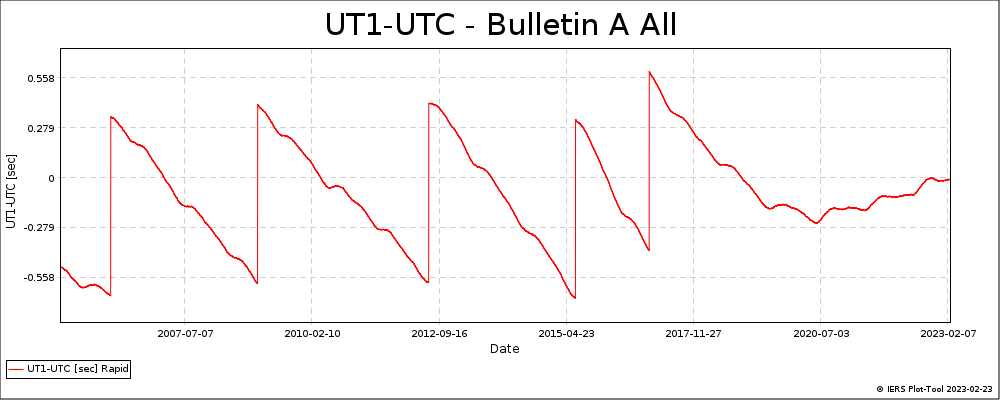
The decision on when to add a leap seconds is handled by the IERS and the current leap seconds situation is available here.
The short summary presented in the previous section should cover everything that's needed for the rest of this post. If you want a more in-depth look at UT0/UT1/UT2 vs UTC vs TAI see [1].
Although designed as such, UTC and leap seconds mechanism are not universally appreciated as a solution. There are currently ongoing discussions that are considering to remove the leap seconds mechanism entirely, with the proposed last leap second being in 2035.
Background: the GNSS
The Global Navigation Satellite System (or GNSS for short) is a combination of several Earth-orbiting satellites that transmit positioning and timing data to GNSS receivers. These receivers then use this data to determine their own location on the Earth's surface. Every time you turn on the "geolocalization" feature of your smartphone, you're using the GNSS. Oftentimes, the term "GPS" is colloquially used to talk about the GNSS, but technically "GPS" is only the constellation of geolocalization satellites managed by the USA. Similarly, there are the Galileo constellation (Europe), the Glonass constellation (Russia) and the Beidou constellation (China).
The problem: GNSS clocks
In order to function properly, each satellite of each constellation needs to maintain a precise time. Moreover, each constellation also needs to find a way to represent this precise time inside the satellite's computer systems and inside the messages they are broadcasting. Luckly, most of the constellation considered in this post chose an epoch+duration representation. Unluckly, they all picked different epochs and there are also some differences on whether they take into account leap seconds.
- GPS clock. Epoch is
05-01-1980 00:00:00 UTC. Leap seconds are ignored. - Galileo clock. Epoch is
22-08-1999 00:00:00 UTC. Leap seconds are ignored. - Beidou clock. Epoch is
01-01-2006 00:00:00 UTC. Leap seconds are ignored. -
Glonass clock. It's different from the others and is defined as
UTC + 3 hours. Since it depends on UTC, it means that leap seconds are taken into account.
Software that works with GNSS data (like receivers and simulators) usually has to also have a way to represent
a UTC time point. Often, that's handled through the POSIX clock. As
stated above, it's epoch is 01-01-1970 00:00:00 UTC (*).
Despite being commonly used to represent UTC time, it does not take into account leap seconds
[3]. This means that it is not a particularly good way to represent
UTC, but it is nevertheless used.
Here the "does not take into account leap seconds" warrants a longer explanation. The behaviour of other clocks (e.g. those based on TAI like the GPS clock) during a leap second is well defined and is intuitive: another second passes. The typical applications in which POSIX time points are used (web servers, database servers, servers in general) generally don't want to have to care too much about leap seconds, yet they still want to use POSIX time points to represent UTC times, because of the ease of using them in the various programming environments.
This, combined with the fact that a POSIX day must always have the same number of POSIX seconds (86400), lead to various "work arounds" which make the behaviour of a POSIX clock around a leap second implementation defined. Some commonly implemented behaviour are:
- Repeating the same POSIX time point during the leap second.
- Spreading the leap second by making many POSIX seconds around the leap second slightly longer than they should be (generally called "leap second smearing").
In order to better understand this, let's see what happens to UTC, TAI and the POSIX clock around a leap second. Let's consider the leap second added on the night between the 1st and the 2nd of January 1980:
| UTC (wall-clock) |
TAI (wall-clock) |
Elapsed UTC seconds (since POSIX epoch) |
POSIX (repeated) |
POSIX (smeared) |
|---|---|---|---|---|
| 01 Jan 1980 23:59:58 | 02 Jan 1980 00:00:16 | 315619216 | 315619198 | 315619198 |
| 01 Jan 1980 23:59:59 | 02 Jan 1980 00:00:17 | 315619217 | 315619199 | |
| 315619199 | ||||
| 01 Jan 1980 23:59:60 | 02 Jan 1980 00:00:18 | 315619218 | 315619199 | |
| 315619200 | ||||
| 02 Jan 1980 00:00:00 | 02 Jan 1980 00:00:19 | 315619219 | 315619200 | |
The first colum is straightforward and shows exactly what we would expect to see on a correct UTC clock: the day has an extra second (23:59:60) and that's the leap second.
The second colum shows that TAI does not handle the leap second in any particular way: it is just another elapsed second. Note that in the first line of the table, TAI is already 18 seconds ahead of UTC, because before this time point other 18 leap seconds have already been added to UTC. On the last line of the table, TAI is 19 seconds ahead of UTC, because a new leap second has elapsed.
The third column shows the number of seconds elapsed since
01-01-1970 00:00:00 UTC (*).
This looks similar to a POSIX time point, but it is different,
because leap seconds count as elapsed seconds.
The fourth and fifth column show two of the possible behaviours of the POSIX clock around a leap second. First of all, we can notice that in the first row there is an 18 seconds difference between the third and the fourth/fifth column. This is the same 18 second difference between the first and the second column and shows what it means that POSIX does not "take into account" leap seconds: although those 18 seconds are by all means elapsed seconds, POSIX time points just ignore them. We can also see that in the last row of the table this difference becomes of 19 seconds, because a new leap second has elapsed.
In the fourth column, the leap second is handled by repeating a POSIX time point twice. This means that a single POSIX time point actually maps to two points on the time line. In the fifth column, the leap second is smeared across multiple POSIX seconds. In this example, it is smeared over just three POSIX seconds for simplicity, but in reality this happens over many more POSIX seconds, so that the difference in the duration of each second is not so strong.
This quirk of the POSIX clock also means that it abuses the definition of "clock" that has been used through the article. To keep this in mind, for the rest of the blog post, let's differentate between the POSIX clock, which behaves as described in the fourth column of the table, from the UTC clock, which instead behaves as described in the third column of the table.
Clock conversions
A common necessity when writing software working with the GNSS is to convert a time point from one clock to another.
Let's assume that we are working with time points represented as epoch and duration. Moreover, let's use the \(t_{clock}\) notation to denote a time point \(t\), expressed as a duration (e.g. number of seconds) elapsed from the \(clock\)'s epoch. Let also \(n_t\) be the number of leap seconds at time \(t\).
Given the table above, and how the introduction of a leap second changes the relationship between the "Elapsed UTC seconds" and the "POSIX (repeated)" columns of the table, the conversion between UTC and POSIX clocks is as follows:
\[ t_{UTC} = t_{POSIX} + n_{t} \]
The next step is to be able to convert from our UTC clock to the GNSS clocks. We can do this by counting how many UTC seconds have elapsed between the POSIX epoch and the epochs of the various GNSS clocks.
Note that this number of elapsed seconds includes leap seconds, and is therefore different from the POSIX timestamp that represents the epoch of the GNSS clock we are considering.
For example, consider the GPS epoch, which has the wall-clock representation
05-01-1980 00:00:00 UTC. This time
point corresponds to the POSIX timestamp
315964800 seconds, but has the timestamp
315964809 seconds in our UTC clock, because
between 01-01-1970 00:00:00 UTC and
05-01-1980 00:00:00 UTC there have been
9 leap seconds (*). [4]
This reasoning can be done for each GNSS epoch and is summarized in the following image (not to scale):
This allows us to write the following conversions:
\[ t_{TAI} = t_{UTC} - 378691210 \, seconds \]
\[ t_{GPS} = t_{UTC} + 315964809 \, seconds \]
\[ t_{Galileo} = t_{GPS} + 619315200 \, seconds \]
\[ t_{Beidou} = t_{Galileo} + 200793600 \, seconds \]
In the image and in the previous equations the Glonass clock is missing. Given its definition relying on a constant offset of three hours from UTC, and that we are already "using" a UTC clock, conversion to it is straightforward:
\[ t_{Glonass} = t_{UTC} + 10800 \, seconds \]
This solves the original problem of converting between the various
GNSS clocks, the POSIX clock and the UTC clock. This is also consistent
with the classes system_clock,
tai_clock,
utc_clock and
gps_clock from the C++'s
std::chrono library
(cppreference docs,
although the Microsoft docs
adds a few more background details).
In fact, as an example, we can take some inspiration from
GCC's implementation
of std::chrono
and define an additional custom chrono clock that handles the Galileo clock and
that can then be used as any other std::chrono
clock (even with std::chrono::clock_cast):
#include <chrono>
template<typename Duration>
using utc_time = std::chrono::time_point<std::chrono::utc_clock, Duration>;
class galileo_clock {
public:
using rep = std::chrono::system_clock::rep;
using period = std::chrono::system_clock::period;
using duration = std::chrono::duration<rep, period>;
using time_point = std::chrono::time_point<galileo_clock>;
static constexpr bool is_steady = false;
static time_point now() { return from_utc(std::chrono::utc_clock::now()); }
template <typename Duration>
static utc_time<std::common_type_t<Duration, std::chrono::seconds>>
to_utc(const std::chrono::time_point<galileo_clock, Duration> &t){
using CDur = std::common_type_t<Duration, std::chrono::seconds>;
return utc_time<CDur> { t.time_since_epoch() }
+ std::chrono::seconds { 315964809 }
+ std::chrono::seconds { 619315200 };
}
template <typename Duration>
static std::chrono::time_point<galileo_clock, std::common_type_t<Duration, std::chrono::seconds>>
from_utc(const utc_time<Duration> &t){
using CDur = std::common_type_t<Duration, std::chrono::seconds>;
return std::chrono::time_point<galileo_clock, CDur> { t.time_since_epoch() }
- std::chrono::seconds { 315964809 }
- std::chrono::seconds { 619315200 };
}
};
This galileo_clock can be easily
adapted to work for Beidou and Glonass by using the numbers reported in the
formulas above.
As an aside, isn't C++ syntax lovely?
With all that templatey angle brackets, I think they really make the code terse. Oh and don't you love how you always have to repeatstd::andstd::chono::everywhere? I know that you have to do it only becauseusingdirectives hopelessly pollute your scope if you use them in headers, but it really makes it clear where each name comes from, even if you're using them fifteen hundred times in five lines. It really makes the code more understandable~. (╯°Д°)╯ ┻━┻
The asterisks
Alas, the story does not end here. As you might have noticed, the whole blog post was sprinkled with asterisks.
As stated above, unless you need to deal precisely with timestamps before 1972 the asterisks shouldn't bother you. However, if you are curious, keep on reading to find out what they are all about.
Those asterisks stem from the following assumptions that are often considered to be true, but technically aren't:
- 1 UTC second is always equal to 1 TAI second
- There have been 10 leap seconds between the TAI epoch and 01-01-1970
- The POSIX epoch is
01-01-1970 00:00:00 UTC - "POSIX time" has always meant what it means now
Let's look at them in detail, starting from the first one. The equivalence
\[ 1 \, \text{UTC second} = 1 \, \text{TAI second} \]
Is true only from the beginning of 1972 onwards. Before that date, leap seconds in the current form did not exist, and the difference between TAI and UTC could be of a fractional number of seconds. Moreover, the length of a TAI second would be different from the length of a UTC second, and the length of a UTC second would change over time.
This proved to be quite cumbersome to maintain, due to the frequent jumps applied to UTC to keep it in sync with UT2 and to the complexity of converting between TAI and UTC.
In the end, it was decided that from 1972 onwards UTC would behave
differently. It would track UT1 (instead of UT2), and 1 UTC second would
last exactly as long as 1 TAI second. A final, irregular jump was applied
to UTC at 01-01-1972 00:00:00 UTC.
This last irregular irregular jump made it so that the time point
01-01-1972 00:00:00 UTC matched
exactly with 01-01-1972 00:00:10 TAI
(note the extra 10 seconds), and from there onwards the two systems would "tick"
at the same speed and be separated by at most an integer number of seconds, leading
to the modern concept of leap seconds. [5]
The 10 second difference between TAI and UTC comes from the slowdown accumulated by UT1 (and therefore UTC) between 1958 (the TAI epoch) and 1972. In other words, it could be said that between 1958 and 1972 there were "in total" 10 leap seconds, which shows why the second assumption stated above is wrong: the 10 leap seconds were between 1958-1972, and not 1958-1970.
We can confirm this by looking at the historical TAI-UTC difference published by the USNO (U.S. Naval Observatory) [6], of which I reported a snippet below:
1965 JUL 1 =JD 2438942.5 TAI-UTC= 3.7401300 S + (MJD - 38761.) X 0.001296 S
1965 SEP 1 =JD 2439004.5 TAI-UTC= 3.8401300 S + (MJD - 38761.) X 0.001296 S
1966 JAN 1 =JD 2439126.5 TAI-UTC= 4.3131700 S + (MJD - 39126.) X 0.002592 S
1968 FEB 1 =JD 2439887.5 TAI-UTC= 4.2131700 S + (MJD - 39126.) X 0.002592 S
1972 JAN 1 =JD 2441317.5 TAI-UTC= 10.0 S + (MJD - 41317.) X 0.0 S
1972 JUL 1 =JD 2441499.5 TAI-UTC= 11.0 S + (MJD - 41317.) X 0.0 S
1973 JAN 1 =JD 2441683.5 TAI-UTC= 12.0 S + (MJD - 41317.) X 0.0 S
1974 JAN 1 =JD 2442048.5 TAI-UTC= 13.0 S + (MJD - 41317.) X 0.0 S
As you can see, the situation before 1972 was quite messy. By using this data, it
can be computed that at 01-01-1970 00:00:00 UTC
the difference between TAI and UTC as of about 8 seconds, not 10 seconds as reported in the
time line image above (and hence the asterisks). [7]
But then there is the question of what happened to those two seconds. In full "worse is better" spirit, the computing world basically decided that UTC before 1972 didn't happen. What was done instead was to take UTC in its post-1972 version and just "roll with it" backwards 1 TAI second (and therefore 1 post-1972 UTC second) at the time.
For example, what Linux currently calls 01-01-1970 00:00:00 UTC
would actually be roughly 01-01-1970 00:00:02 UTC if we use
the real UTC as it was defined between 1970 and 1972, as shown by the following diagram:
Note that, after 1972, "Linux" UTC and "real" UTC behave in the same way. Given this, a more precise definition of POSIX time would be "the number of TAI seconds elapsed since 1972-01-01 00:00:00 (real) UTC, plus the amount of TAI seconds in two TAI years, minus the amount of leap seconds since 1972", which is quite a mouthful. This difference between "real" UTC and "Linux" UTC is why the third assumption mentioned at the beginning of this section is false.
Sources for this are surprisingly sparse. Besides Taylan Kammer's notes on the subject (who I should also thank for the kind emails that helped me solving this conundrum) and a few random tibits here and there I couldn't find much.
Therefore, I decided to look for the authoritative source of thruth: the source
code for the time() system call
on a recent version of Linux (commit
2fcd07b7ccd5fd10b2120d298363e4e6c53ccf9c
at the time of writing).
Now, I am not familiar at all with the Linux kernel source code, so take whatever follows
with a huge grain of salt.
However, it seems that the time
syscall is just a
thin wrapper
around ktime_get_real_seconds.
This in turn seems to
"just" return the xtime_sec field of an instance of the
timekeeper struct
which seems to be initialized in the
timekeeping_init method.
This method in turn defers to read_persistent_wall_and_boot_offset which in turn
calls read_persistent_clock64 from
rtc.c file of the specific architecture (x86 in our case).
This uses the get_wallclock method of the
x86_platform_ops struct,
which is bound to mach_get_cmos_time
(source).
which in turn calls
mc146818_get_time. This function
(with a few more in-between steps) reads directly the current time set in the CMOS chip.
The tm struct read from the CMOS represents the
time as year-month-day hour-minute-seconds, as we can see both from the struct's fields names
and the MC146818 datasheet.
The kernel needs to convert this to POSIX time, and we can see that it does so
at the end
of mach_get_cmos_time by calling
rtc_tm_to_time64. This
in turns calls
mktime64 and
there
our journey ends.
mktime64 does a very straightforward
conversion, which assumes that all minutes have the same length (so no leap seconds)
and, more importantly for our question, that every second ever has always had the same length.
We finally have a first-hand source confirming what's going on with POSIX time before 1972,
at least on the Linux kernel version identified by that commit. If we wanted to be really
thorough we would also have to check all the other architectures, but I'll call this good enough.
This leaves us with the fourth assumption, that "POSIX time" has always meant what it means now. Also this is not true.
Although probably here we may have to make a distinction between POSIX time and UNIX time. I don't know that and didn't want to go down *that* rabbit hole.
If we go back to 1971 and look at the First Edition's Unix Programmer's Manual we will see that originally, "UNIX time" was measured in sixtieths of a second since midnight, 1st January 1971:
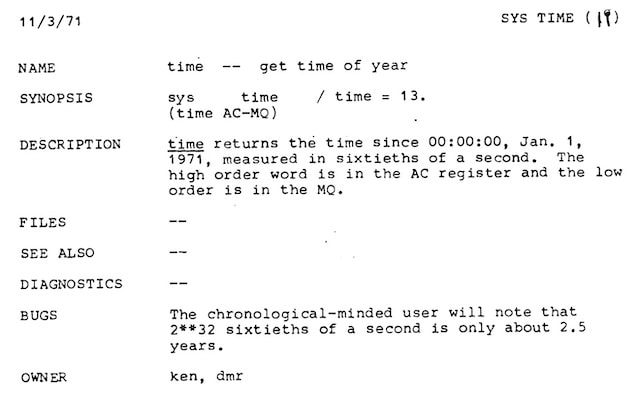
The definition of "UNIX time" changed in 1972, when it was modified to still return the sixtieths of a second, but since midnight, 1st January 1972. It was changed again in 1973 to the current definition (with the exception of referencing GMT instead of UTC). [8].
This means that the answer to the question "what's the POSIX time of this time point" has different answers depending on when you ask it, and puts the final nail in the coffin in the idea of using POSIX time for representing dates before 1973 if you need to be precise.
Conclusions
All of this started with an easy question: how to convert a POSIX timestamp to a GPS time timestamp. As in the best of traditions, finding the correct answer to this required a surprising amount of historical context, which I am happy to have summarized here (despite the absurd time commitment that this required).
Feel free to use the material reported in this post for whatever project you're working on, but please link back to this blog post if you share it publicly.
References
[1]
I didn't want to invest more time into wasn't able to find
a precise, authoritative definition of TAI/UT1/UTC. I relied on various
other Internet things I found (a,
b,
c,
d).
↵
[3] POSIX standard and Stackoverflow answer regarding POSIX time and leap seconds ↵
[4] Stackoverflow answer concerning this. Not all answers to the question are equally correct. ↵
[6] The conversion table published by USNO. ↵
[7] The 8 seconds ↵
[8] A very helpful Stackoverflow summary and another blog post with more rabbit holes to dig into if you're interested. ↵